|
Algebraic Transformations
Transforming algebraic equations and expressions is fundamental to symbolic computation. Although this page refers to the Sym application, it might be useful to anyone interested in symbolic computation. Sym is free, open source code software. Consider the following simple case.
You have an expression to be transformed:
a*(b+c*d)
And a transform you want to apply, here's the basic distributive law, expressed as a Sym transform.
f1*(f2+f3)~f1*f2+f1*f3
You apply the transform with Sym and get the following result:
a*b+a*c*d
How does the Transform class transform equations and expressions this way? To understand it's operation, first divide the transform into two pieces. The 'matchToMe' side on the left of the '~', and the 'outPattern' on the right of the '~'. The expression, and both sides of the transform are parsed into individual trees. The expression to be transformed can be visualized as:
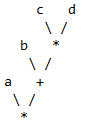 figure 1. figure 1.
Tree data structures are common in computer programming. You might want to Google the concept if you are unfamiliar with them. The left side of the transform can be visualized as:
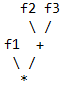 figure 2. figure 2.
The transform class will walk the tree shown in figure 2, and while doing so will check to see if there are matching nodes in figure 1. Clearly the '*' and '+' in figure 2 have corresponding nodes in figure 1. There are suitable functions that f1, f2, and f3, can represent. So this transformation can proceed. The following assignments will be made:
f1=a
f2=b
f3=c*d
The right hand side of the transform is used as a template.
f1*f2+f1*f3
The f1, f2, and f3 variables of this template are replaced by the assignments above. The result is:
a*b+a*c*d
Sym can use tree like transforms of any complexity with regards to the number of binary and unary operations. It can also apply the transform to any branch of the expression to be transformed. Download the latest code too see the details.
Here is a list of algebraic transformation expressions in the format Sym uses.
Symbolic Computation, Laws of Algebra, open source code.
a+b~b+a
a+b+c~a+c+b
a-b~-b+a
a*b~b*a
a*b*c~a*c*b
a==b~b==a
a*(b+c)~(a*b+a*c)
a*b+a*c~a*(b+c)
a/c+b/c~(a+b)/c
(a+b)/c~(a/c+b/c)
a*b==c~a==c/b
a+b==c~a==c-b
a-b==c~a==c+b
a/b==c~a==c*b
-a==b~a==-b
a*b==a*c~b==c
a+b==a+c~b==c
b-a==c-a~b==c
b/a==c/a~b==c
a-b==a-c~b==c
a/b==a/c~b==c
a/b==c~b==a/c
a-a~0
a/a~1
a+0~a
a*1~a
a*0~0
(a)+b~a+b
(a)-b~a-b
(a)*b~a*b
(a)/b~a/b
a-(-b)~a+b
a+(-b)~a-b
a*(-b)~a*-b
a/(-b)~a/-b
((a))~(a)
-a*-b~a*b
(-a)*b~-a*b
(a)==b~a==b
Pow((Pow(x,m)),n)~Pow(x,(m*n))
Pow(x,1)~x
Pow(x,0)~1
Pow(x,(-1))~1/x
Pow(x,m)*Pow(x,n)~Pow(x,(m+n))
Pow(x,m)/Pow(x,n)~Pow(x,(m-n))
Pow((x*y),n)~Pow(x,n)*Pow(y,n)
Pow((x/y),n)~Pow(x,n)/Pow(y,n)
Pow(x,(-n))~1/Pow(x,n)
Pow(a+b,2)~Pow(a,2)+2*a*b+Pow(2,2)
Pow(a-b,2)~Pow(a,2)-2*a*b+Pow(2,2)
Pow(b,y)==x~y==Log(x,b)
Log(x,b)==y~Pow(b,y)==x
Pow(x,y)==a~x==Pow(a,1/y)
Pow(Sqrt(a),2)~a
Sqrt(Pow(a,2))~a
Pow(a,(b))~Pow(a,b)
Pow((a),b)~Pow(a,b)
Sin(x)/Cos(x)~Tan(x)
Sin(Asin(x))~x
Cos(Acos(x))~x
Tan(Atan(x))~x
Pow(Sin(x),2)+Pow(Cos(x),2)~1
Sin(fx)==fy~fx==Asin(fy)
Cos(fx)==fy~fx==Acos(fy)
Tan(fx)==fy~fx==Atan(fy)
Asin(fx)==fy~fx==Sin(fy)
Acos(fx)==fy~fx==Cos(fy)
Atan(fx)==fy~fx==Tan(fy)
Home
Sym
Online Solvers
Code
Custom Software
Contact
Copyright 2012 SymbolicComputation.com
|

